Question

The power company routes its lines as shown in the illustration. How much wire ( in yards) could be saved by going directly from A to E? yd

Answer 1

To solve this question we will use the following diagram:

Using the Pythagorean theorem for triangle AEO we get:

`AE^2=AO^2+EO^2\text{.}`

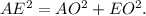
Substituting AO=68 yd, and EO=285 yd we get:

`\begin{gathered} AE^2=(68yd)^2+(285yd)^2, \\ AE^2=4624yd^2+84225yd^2, \\ AE^2=85849yd^2, \\ AE^2=293^2yd^2\text{.} \end{gathered}`

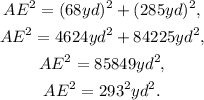
Therefore AE=293 yd. Now, the wire required for the long path is:

`38yd+304yd+30yd+19yd=391yd\text{.}`

Therefore you could save:

`391yd-293yd=98yd`

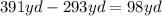
taking the short route.

Answer: 98yd.