Question

In parallelogram RODY, angle R = (7x + 22) and angle O = ( 9x – 2 ) . What is the measure of angle R?

Answer 1

6Hello there. To solve this question, we'll have to remember some properties about parallelograms.

Given the parallelogram RODY, and the measure of the angles as functions of a variable x:

`\begin{gathered} m\angle R=(7x+22)^(\circ) \\ m\angle O=(9x-2)^(\circ) \end{gathered}`

We have to determine the measure of the angle R.

For this, we'll have to remember the following property about parallelograms:

The sides with one and two lines have the same measure, respectively.

Now imagine the following angles:

And that we move this triangle to the other side, that is:

With this, you notice that the angles might be supplementary, or mathematically it is the same as:

`\alpha+\beta=180^(\circ)`

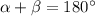
We also know that the angle at R might be:

When we moved the triangle, we now have that:

`m\angle R-(90^(\circ)-\alpha)=m\angle R-90^(\circ)+\alpha=90^(\circ)\Rightarrow m\angle R=180^(\circ)-\alpha=\beta`

So the measure of the angle at O will be:

`m\angle O=\alpha`

In the end, we reached the equation we need to solve:

`m\angle R+m\angle O=180^(\circ)`

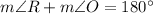
Plugging the measures in function of x, we get

`(7x+22)^(\circ)+(9x-2)^(\circ)=180^(\circ)`

Add the values

`16x+20^(\circ)=180^(\circ)`

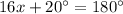
Subtract 20º on both sides of the equation

`16x=160^(\circ)`

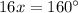
Divide both sides of the equation by a factor of 16

`x=10^(\circ)`

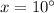
Now, to find the measure of the angle R, simply plug the value of x:

`m\angle R=(7\cdot10+22)^(\circ)=(70+22)^(\circ)=92^(\circ)`

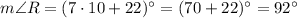
This is the answer we were looking for.

is:

With this, you notice that the angles might be supplementary, or mathematically it is the same as: