Given the expression:
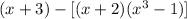
You can simplify it as follows:
1. Apply the FOIL Method to multiply the binomials inside the square brackets. This method states that:
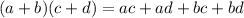
You need to remember the Sign Rules for Multiplication:
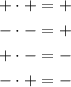
It is important to remember that, according to the Product of Powers Property, you need to add the exponents when you multiply powers with the same base.
Then, you get:
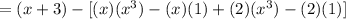
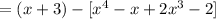
2. Distribute the negative sign:
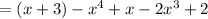
3. Add the like terms:
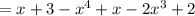
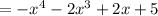
Hence, the answer is: Option A.