Step-by-step explanation
The standart form
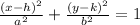
h and k represents the center of the ellipse, in this case.
The center of the ellipse is the point (0, 0)
a represents the distance between the center and the vertex, in this case
The value for a is: 9
b represents the distance between the center and the co-vertex, in this case
The value for b is: 3
Answer
The center of the ellipse is the point (0, 0)
The value for a is: 9
The value for b is: 3