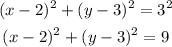Question

What is the equation of a circle with center (2.3) that passes through the point (5.3) (x - 2)2+(y - 3)2 = 3 (x - 5)²+(y - 3)2 = 3( x-2)2+(y-3)=9 (x-5)+ (y - 3) = 9

Answer 1

(x - 2)² + (y - 3)² = 9

Step-by-step explanation

The equation of a circle with center (h, k) and radius r is

`(x-h)^2+(y-k)^2=r^2`

In this problem, the center of the circle is point (2, 3) and we don't know the radius, but we do know a point where the circle passes (5, 3). The distance between the center and this point is the radius of the circle:

Since the center and the point are at the same y-coordinate, the distance - and therefore the radius - is the difference between the x-coordinates of the two points:

`r=5-2=3`

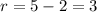
The equation then is:

`\begin{gathered} (x-2)^2+(y-3)^2=3^2 \\ (x-2)^2+(y-3)^2=9 \end{gathered}`