We have
x is the number of hour working as a lifeguard
y is the number of hour washing cars
The first inequality is
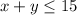
we isolate the y
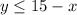
the second inequality is
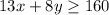
then we isolate the y
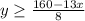
then we will plot the inequalities
We have as a solution the area where the two areas intercept each other
One solution to these systems of inequalities could be
x=12
y=2
Julian could work 12 hours lifeguarding and 2 hours washing cars