SOLUTION:
Case: Probabilities
Given: Probabilty of obtaining events (1, 2, 3, 4, or 5 classes)
Required: To find:
the following probabilities for a student selected at random:
a.) What is the probability that a student is taking 2 or more classes?
b.) What is the probability that a student is taking at least 3 classes?
c.) What is the probability that a student is taking more than 3 classes?
d.) What is the probability that a student is taking less than 2 classes?
e.) What is the probability that a student is taking no more than 2 clases?
f.) What is the average (mean) amount of classes a student takes at BHCC?
g.) What is the standard deviation for the amount of classes a student takes at BHCC?
Final answer:
a) Pr(taking 2 or more classes) = 0.28+ 0.15+ 0.31+ 0.07 gives 0.81
b) Pr (taking at least 3 classes) = 0.15+ 0.31+ 0.07 gives 0.53
c) Pr (taking more than 3 classes) = 0.31+ 0.07 gives 0.38
d) Pr (taking less than 2 classes) = 0.19
e) Pr (taking no more than 2 classes) = 0.19 + 0.28 gives 0.47
f) Average
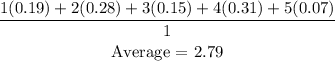
g) Standard deviation
![\begin{gathered} \operatorname{mean}deviation \\ d=\text{ }\sqrt[]{(0.19(1-2.79)^2+0.28(2-2.79)^2+0.15(3-2.79)^2+0.31(4-2.79)^2+0.07(5-2.79)^2)/(1)} \\ \\ d\text{ = }\sqrt[]{1.5859} \\ d\text{= 1.2}6 \end{gathered}]()