Question

Alie detector will show a positive reading (indicate a lie) 5% of the time when the person is telling the truth and 98% of the time when the person is lying. Suppose two people are suspects in a one person crime and (for certain) one is guilty and will lie. Assume further that the lie detector operates independently for the truthful person and the liar. What is the probability that the detector is completely wrong that is that it gives a positive reading for the innocent suspect and a negative reading for the guilty suspect.

Answer 1

- Let M be the event that the machine detects someone is lying

- Let L be the event that the person is actually lying.

- The question tells us that the lie detector will detect a lie 5% of the time if the person is telling the truth.

- This means that the probability that the machine detects a lie given that the person is telling the truth is 5%. This is a conditional probability

- Mathematically, we have:

`\begin{gathered} P(M|L^c)=5\text{ \%}=(5)/(100)=0.05 \\ \text{where,} \\ L^c\text{ is the complement of L, that is, the event that the person is telling the truth} \end{gathered}`

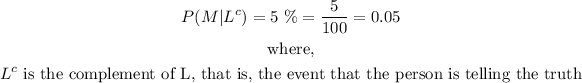
- Next, we are told that the machine detects a lie 98% of the time when the person is actually lying.

- This implies that the probability that the machine detects a lie given that the person is lying is 98%.

- Mathematically, we have:

`P(M|L)=98\text{ \%}=(98)/(100)=0.98`

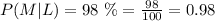
- The question asks us for the probability that the detector is completely wrong and gives a positive reading for an innocent suspect and negative reading for the guilty.

- We can also rework this question in familiar conditional probability language as follows:

- We are to find the probability that the lie detector detects a lie given that the innocent person is telling the truth AND the probability that the detector detects nothing for the guilty person given that he lied.

- We should break down this sentence into two aspects and then bring them back together with the AND probability formula. The AND probability formula is given below:

`\begin{gathered} \text{Given events A and B, we have that the AND probability for both events is given as:} \\ P(A\text{ AND }B)=P(A)* P(B)_{} \end{gathered}`

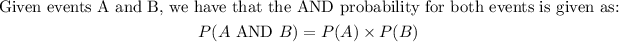
- Now, let us break down the sentence into two.

Sentence 1:

"We are to find the probability that the lie detector detects a lie given that the innocent person is telling the truth"

This statement corresponds to the probability we had earlier:

`P(M|L^c)=0.05`

Sentence 2:

"...the probability that the detector detects nothing for the guilty person given that he lied."

- This is just the complement of the other probability we had earlier:

`\begin{gathered} \text{ Earlier, we had} \\ P(M|L)=0.98 \\ \text{Now, we have} \\ P(M^c|L) \\ \\ \text{But we know that complements add up to 1} \\ \\ P(M|L)+P(M^c|L)=1 \\ 0.98+P(M^c|L)=1 \\ \text{Subtract 0.98 from both sides} \\ \\ P(M^c|L)=1-0.98 \\ P(M^c|L)=0.02 \end{gathered}`

- Thus, we can now apply the AND probability formula to combine our two results as follows:

`\begin{gathered} \text{if A}=M|L^c\text{ and }B=(M^c|L) \\ \text{Then,} \\ P(A\text{ AND B)}=0.02*0.05=0.001 \end{gathered}`

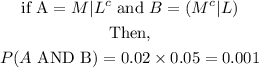
Final Answer

The probability that the detector gives a positive reading for the innocent suspect and a negative reading for the guilty suspect, is 0.001