Question

Find the point that partitions the segment AB with coordinates A(-2, 4) and B(7,-2) in the ratio 1:2.P: (2, 1)P: (3, 1)P: (1,2)P: (1,3)

Answer 1

Given :

First point (A) = (-2,4)

Second point (B) = (7,-2)

ratio is 1:2

If the point is :

`\begin{gathered} (x_1,y_1)_{} \\ \text{and} \\ (x_2,y_(2)) \end{gathered}`

line sigmrnt ratio is m:n then point is:

`(x^(\prime),y^(\prime))=((mx_1+nx_2)/(m+n),(my_1+ny_2)/(m+n))`

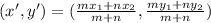
If

`\begin{gathered} m=1 \\ n=2 \\ x_1=-2 \\ x_2=7 \\ y_1=4 \\ y_2=-2 \end{gathered}`

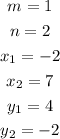
a partition of AB in ratio 1:2

So "B" point distance from A point is:

`\begin{gathered} =7-(-2) \\ =7+2 \\ =9 \end{gathered}`

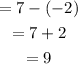
ratio is 1:2 would be divide is 1/3.

so distance 9 is:

`(9)/(3)=3`

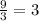
Coordinates form A point is:

`\begin{gathered} =3+(-2) \\ =3-2 \\ =1 \end{gathered}`

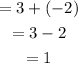
Y coordinates B point to A point is:

`\begin{gathered} =4-(-2) \\ =4+2 \\ =6 \end{gathered}`

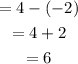
Ratio is 1:2 that mean:

`\begin{gathered} =(6)/(3) \\ =2 \end{gathered}`

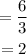
y coordinates from A point is:

`\begin{gathered} =4-2 \\ =2 \end{gathered}`

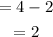
So the point is (1,2)