The density is equal to the quotient between the weight and the volume of the board.
We can calculate the volume of the board as the volume of a rectangular prism: width by length by thickness.
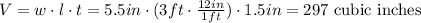
Then, if we divide the weight by the volume, we get:
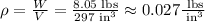
If we express the density in pounds per cubic feet, we can write:
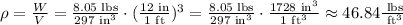
Answer: the density is 46.84 pounds per cubic feet.