Question

65% of men consider themselves knowledgeable soccer fans. If 12 men are randomly selected, find the probability that exactly 7 of them will consider themselves knowledgeable fans. Also, calculate the mean and standard deviation of this binomial distribution.

Answer 1

Question 1:

The probability that 7 men would consider themselves knowledgeable is 0.20392

Question 2:

The Mean and Standard Deviation of the distribution are 7.8 and 1.6523

SOLUTION

Problem Statement

We are told 65% of men consider themselves knowledgeable soccer fans. We are told that 12 men are randomly chosen.

1. We are required to find the probability that 7 of them will consider themselves knowledgeable.

2. We are also required to find the mean and standard deviation of this survey of 12 men.

Method

To solve this question, we need to know 3 things outlined below:

1. Binomial probability formula:

This formula is used to calculate the probability of a particular event occurring after multiple trials. In the case of this question, one event is asking 1 man if he considers himself knowledgeable. Thus, asking 12 men results in multiple trials and leads to Binomial probability being invoked.

The formula to calculate this probability is:

`\begin{gathered} P=^nC_rp^rq^(n-r) \\ \text{where,} \\ p=\text{probability of success (In this case, probability of 7 men claiming to be knowledgeable)} \\ q=\text{probability of failure}=1-p \\ n=\text{ Number of possible trials (In this case, 12)} \\ r=\text{ Number of occurrence of an event (In this case, 7)} \end{gathered}`

2. Mean of a Binomial distribution:

`\begin{gathered} \mu=np \\ \text{where,} \\ n=\text{ Number of possible trials} \\ p=\text{ }The\text{ probability of success.} \end{gathered}`

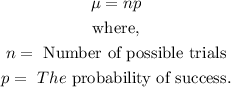
3. Standard deviation of a Binomial Distribution

`\sigma=\sqrt[]{\text{npq}}`

Implementation

Question 1:

The probability that 7 of the men will consider themselves knowledgeable is:

`\begin{gathered} p=65\text{ \%}=(65)/(100)=0.65 \\ q=1-p=1-(65)/(100)=0.35 \\ n=12 \\ r=7 \\ \\ \therefore P=^nC_rp^rq^(n-r) \\ P=^(12)C_7*0.65^7*0.35^(12-7) \\ P=792*0.0490223*0.0052522 \\ P=0.20392 \end{gathered}`

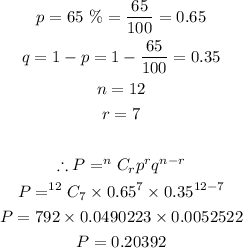
Therefore, the probability that 7 men would consider themselves knowledgeable is 0.20392

Question 2:

The Mean and Standard deviation are gotten as follows:

`\begin{gathered} p=0.65 \\ n=12 \\ q=1-p,q=1-0.65\implies q=0.35 \\ \\ \therefore Mean(\mu)=np=0.65*12=7.8 \\ \\ \text{ Standard deviation (}\sigma)=\sqrt[]{\text{npq}}=\sqrt[]{12*0.65*0.35} \\ \therefore\sigma=1.6523 \end{gathered}`

Final Answer

Question 1:

The probability that 7 men would consider themselves knowledgeable is 0.20392

Question 2:

The Mean and Standard Deviation of the distribution are 7.8 and 1.6523