We have the following perfect squares less than 100:
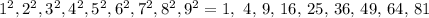
We have the following perfect cube less than 100:
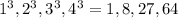
The only number that is in both lists, besides 1, that is at the same time perfect square and the perfect cube is number 64. This number is the square of 8, and the cube of 4.
Therefore, the number 64 is a perfect square and a perfect cube less than 100 (besides 1).