ANSWER:
2160 cm^3
Explanation:
To calculate the volume of the figure, we must divide it in two, the upper part would be a triangular prism and the lower part a quadrangular prism.
The volume of a prism in both cases is the area of the base of the figure multiplied by the length, therefore:
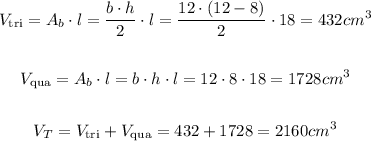
The volume of the figure is 2160 cm^3
A cross section is a 2-dimensional "cut" in a 3-dimensional figure. Therefore, if it is vertical, the figure would be the base of the figure and if it is a horizontal cut, it would be a square.