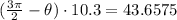Given :
a bug sits 10.3 inches from the center of rotation on one of its blades.
So, the radius = r = 10.3
At first, The bug is at the 3 o'clock position on the fan when it begins to turn.
the length of the arc = θ * r
when , the bug sits 4.5 inches to the right of the vertical diameter of the fan for the second time.
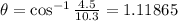
So, the length of the arc =

Note : for the second time the angle will be ( 2pi - θ )
b. when the bug 4.7 inches to the left of the vertical diameter of the fan for the first time.
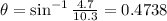
So, the length of the arc =
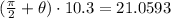
C. when the bug 4.7 inches to the left of the vertical diameter of the fan for the second time.
So, the length of the arc =