Question

Select the correct answer. What is the value of y in this linear system? 41 - 2y + 3z = 1 80 - 3y + 5z = 4 71 - 2y + 4z = 5 O A. 3 OB. 0 O C. 1 o D. -1 Reset Next Al rights reserved.

Answer 1

Solve the given simultaneous equation to find the value of y:

`\begin{gathered} \begin{cases}4x-2y+3z=1 \\ 8x-3y+5z=4 \\ 7x-2y+4z=5\end{cases} \\ \text{Multiply the first equation by 2 to get: } \\ 8x-4y+6z=2 \end{gathered}`

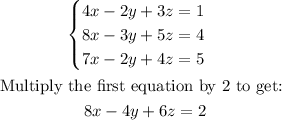
Subtract the new equation from the second equation:

`\begin{gathered} \begin{cases}8x-3y+5z=4 \\ 8x-4y+6z=2\end{cases} \\ \text{Subtract to get:} \\ -3y-(-4y)+5z-6z=4-2_{} \\ \Rightarrow-3y+4y-z=2 \\ \Rightarrow y-z=2 \end{gathered}`

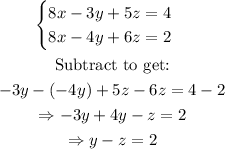
Multiply the first equation by 7 and the last equation by 4, then subtract:

`\begin{gathered} \begin{cases}28x-14y+21z=7 \\ 28x-8y+16z=20\end{cases} \\ \text{Subtract the second equation from the first:} \\ \Rightarrow-14y-(-8y)+21z-16z=7-20 \\ \Rightarrow-6y+5z=-13 \end{gathered}`

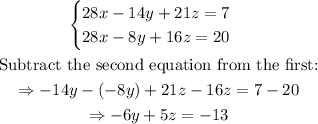
Combine this equation with the first one derived, y-z=2.

`\begin{gathered} \begin{cases}-6y+5z=-13 \\ y-z=2\end{cases} \\ \text{Multiply the second equation by 5:} \\ \begin{cases}-6y+5z=-13 \\ 5y-5z=10\end{cases} \\ Add\text{ the equations:} \\ \Rightarrow-6y+5y+5z-5z=-13+10 \\ \Rightarrow-y=-3 \\ \text{Divide both sides by -1:} \\ \Rightarrow y=3 \end{gathered}`

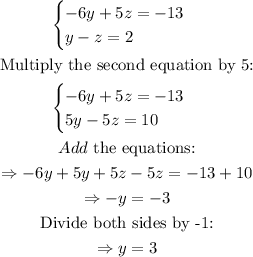
Hence, the value of y is 3.

The correct option is A.