Question

A certain shampoo is available in two sizes. A 14.2-ounce bottle costs $3.98. A 33. 9-ounce bottle costs 59.98.Find the unit price for each size. Then state which size is the better buy based on the unit price.Round your answers to the nearest cent.Unit price for the 14.2-ounce bottle:Unit price for the 33.9-ounce bottle:siper ounce$ per ounceThe better buy:The 14.2-ounce bottleThe 33.9-ounce bottleNeither (They have the same unit price)

Answer 1

So we need to calculate the unit price for each bottle of shampoo. The unit price in this case is the price per ounce i.e. the amount of money that each ounce costs in that bottle. This quantity is calculated by taking the total price of the bottle and dividing it by the ounces of shampoo it has:

`\text{Unit price}=\frac{\text{cost of the bottle}}{\text{ounces in the bottle}}`

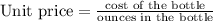
Then for the 14.2oz bottle we have:

`\text{Unit price}=\frac{\text{cost of the bottle}}{\text{ounces in the bottle}}=\frac{\text{\$}3.98}{14.2oz}=\text{\$0.28 per ounce}`

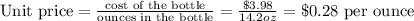
Then for the 33.9oz bottle we get:

`\text{Unit price}=\frac{\text{cost of the bottle}}{\text{ounces in the bottle}}=\frac{\text{\$}59.98}{33.9oz}=\text{\$}1.77\text{ per ounce}`

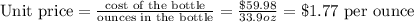
Then the unit price for each size and first pair of answers are:

Unit price for the 14.2-ounce bottle: $0.28

Unit price for the 33.9-ounce bottle: $1.77

Then we have to decide which is a better buy. The answer is simple: the one with the lowest unit price. This would be the 14.2-ounce bottle. Then the last answer is the first of the three options:

-The 14.2-ounce bottle

-The 33.9-ounce bottle

-Neither (They have the same unit price)