Question

=If P = (-2, -1) and Q = (-6,-3) are thendpoints of the diameter of a circle,find the equation of the circle.(x - [?])2 + (y - [])2-X--==

Answer 1

Case: Circle equations

Method:

The endpoints of the diameter are P(-2, -1) and Q(-6, -3)

The diameter therefore:

`\begin{gathered} d^2=(-6--2)^2+(-3--1)^2 \\ d^2=(-6+2)^2+(-3+1)^2 \\ d^2=(-4)^2+(-2)^2 \\ d^2=16+4 \\ d^2=20 \\ d=√(20) \\ d=√(4*5) \\ d=2√(5) \end{gathered}`

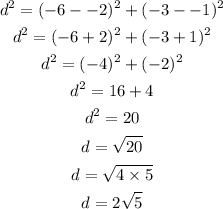
The radius therefore is:

`\begin{gathered} diameter=2√(5) \\ radius \\ r=(2√(5))/(2) \\ r=√(5) \end{gathered}`

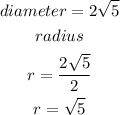
The equation of a circle is given as:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ (x-a)^2+(y-b)^2=(√(5))^2 \\ (x-a)^2+(y-b)^2=5 \end{gathered}`

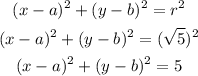
The center (a, b) is the midpoint between P and Q

`\begin{gathered} x_m=(x_1+x_2)/(2) \\ x_m=(-2-6)/(2) \\ x_m=(-8)/(2) \\ x_m=-4 \\ AND \\ y_m=(y_1+y_2)/(2) \\ y_m=(-1-3)/(2) \\ y_m=(-4)/(2) \\ y_m=-2 \\ The\text{ }center \\ (-4,-2) \end{gathered}`

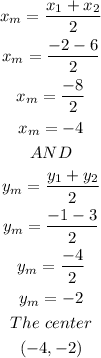
The center (a,b) is (-4, -2)

Final answer:

`(x-[-4])^2+(y-[-2])^2=5`