Answer:
The second option is the best option
Step-by-step explanation:
Given the dimensions of the roll in the first option;
Length(l) = 10 feet
Width(w) = 10 feet
So the area(A) of the roll is;
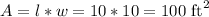
Given the cost per square foot as $3.50, therefore the cost for 100 square feet roll will be $350
Given the dimensions of the roll in the second option as;
Length (l) = 11 feet
Width (w) = 9 feet
So the area(A) of the roll is;
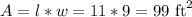
Given the cost per square foot as $3.25, therefore the cost for 99 square feet roll will be $321.75
We can see that the second option is cheaper since she would have to spend $321.75 for the roll as against a roll that cost $350 for the first option.
So the second option is the best option.