Question

I need help pleasesee

Answer 1

We have the following problem:

We know that x=25° and y=55°, therefore we can know the value of alpha, since

`\begin{gathered} x+y+\alpha=180 \\ 25+55+\alpha=180 \\ 80+\alpha=180 \\ \alpha=180-80 \\ \alpha=100 \end{gathered}`

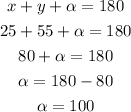
We also notice that since the higway is straight and the plane is flying in an horizontal path this lines area parallel, then

`\begin{gathered} x=\beta \\ y=\gamma \end{gathered}`

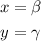
this follows from the fact that this angles are alternate with each other.

Once we know the values of the angles we are prepared to find the distance from tha plane to point A. Using the Law of sines we know that

`(\sin\alpha)/(a)=(\sin \gamma)/(c)`

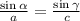
where, in this case, a=6 mi and c is the distance we are looking for. Plugging the values we know and solving for c we have

`\begin{gathered} (\sin100)/(6)=(\sin 55)/(c) \\ c=(\sin 55)/(\sin 100)(6) \\ c=4.99 \end{gathered}`

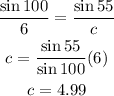
Therefore the distance from the plane to point A is 4.99 mi.

Any questions so far?