Question

Which of the plotted points on the graph represent the zeros of the function f f(x) = (x2 + 2x – 8)(x - 6)? Select all that apply. A. (2,0) В. (6, 0) D. (-4,0) E. € 6,0) F. (0, 2) G. (0,8)

Answer 1

We have the function:

`f(x)=(x^2+2x-8)(x-6)`

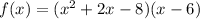
We already have one of the roots (x=6).

We can factorize the quadratic factor in order to find the other roots:

`\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4\cdot1\cdot(-8)}}{2} \\ x=-1\pm\frac{\sqrt[]{4+32}}{2} \\ x=-1\pm\frac{\sqrt[]{36}}{2} \\ x=-1\pm(6)/(2) \\ x=-1\pm3 \\ x_1=-1-3=-4 \\ x_2=-1+3=2 \end{gathered}`

We then can write f(x) as:

`f(x)=(x+4)(x-2)(x-6)`

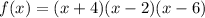
being the zeros x=6, x=-4 and x=2.

In coordinates, this zeros are represented by the points (6,0), (-4,0) and (2,0).

Answer:

A. (2,0)

В. (6, 0)

D. (-4,0)