Question

I missed class yesterday. we have an assignment to do. i don’t understand and need help.

Answer 1

The given system is:

`\begin{gathered} 8x+11y=37 \\ 8x+y=7 \end{gathered}`

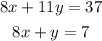
Notice that the coefficients of x in both equations are the same.

Therefore, Subtract the first equation form the second to eliminate the variable x:

`\begin{gathered} 8x-8x+11y-y=37-7 \\ 10y=30 \\ y=(30)/(10)=3 \end{gathered}`

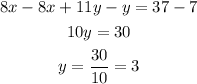
Substitute y = 3 into the second equation:

`\begin{gathered} 8x+3=7 \\ 8x=7-3=4 \\ x=(4)/(8)=(1)/(2) \end{gathered}`

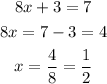
Hence, the solution of the system is:

x = 1/2 and y = 3