Given:
The length of the rectangle is,
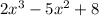
The width of the rectangle is,
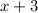
To find:
The number of terms in the area of the rectangle.
Step-by-step explanation:
The area of the rectangle is
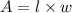
Substituting the given values we get,
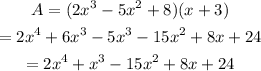
Therefore, the polynomial has 5 terms.
Final answer:
The polynomial has 5 terms.