The Solution:
Let the rate with no wind be represented with x.
And let the rate of the wind be represented with y.
Given:
With no wind:
distance (d) = 1152 miles
time (t) = 4 hours
rate with no wind = x-y
By formula,
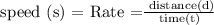
Substituting these values, we get
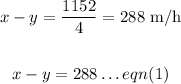
Finding the rate with the wind:
distance = 1152 miles
time(t) = 3.2 hours
rate = x+y
Substituting these values, we get

Solving the pair of equations simultaneously, we get
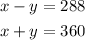
By the Elimination Method, we shall add the corresponding terms in both equations.
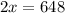
Dividing both sides by 2, we get
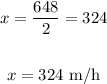
Thus, the rate of the airplane with no wind is 324m/h.
To find the rate of the wind:
We shall substitute 324 for x in eqn(2).
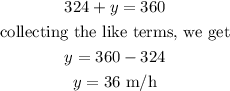
Therefore, the rate of the airplane with no wind is 324m/h.
The rate of the wind is 36 m/h.