Question

GRAPH the parabola.y=-x^2+6Plot 5 points on the parabola: the vertex, two points on the left of the vertex, and two points in the right of the vertex

Answer 1

Given: The function below

`y=-x^2+6`

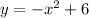
To Determine: The graph of the parabola and the vertex

Solution

Determine the vertex

The vertex form of a parabola is

`\begin{gathered} y=a(x-h)^2+k \\ vertex=(h,k) \end{gathered}`
`\begin{gathered} h=-(b)/(2a) \\ k=f(-(b)/(2a)) \end{gathered}`

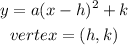
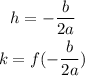
Note:

`\begin{gathered} If \\ ax^2+bx+c=0 \\ y=-x^2+6 \\ a=-1,b=0,c=6 \end{gathered}`
`\begin{gathered} Therefore \\ h=(-(0))/(2*-1)=0 \\ y=-x^2+6 \\ when,x=0 \\ y=-0^2+6 \\ y=0+6 \\ y=6 \end{gathered}`

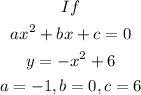
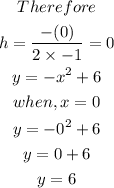
The coordinate of the vertex is (0, 6)

Let us take two points on the left

`\begin{gathered} x=-2 \\ y=-(-2)^2+6 \\ y=-4+6 \\ y=2,(-2,2) \\ x=-1 \\ y=-(-1)^2+6 \\ y=-1+6 \\ y=5(-1,5) \end{gathered}`

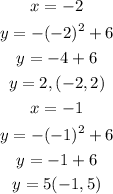
Let us take two points on the right

`\begin{gathered} x=1 \\ y=-(1)^2+6 \\ y=-1+6 \\ y=5,(1,5) \\ x=2 \\ y=-(2)^2+6 \\ y=-4+6 \\ y=2,(2,2) \end{gathered}`

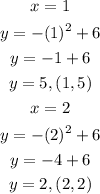
Let us plot the 5 points as a graph as shown below

Hence, the vertex is (0, 6) and two points on the left of the vertex are (-1,5) and (-2, 2), and two points to the right of the vertex are (1, 5) and (2, 2)