Since we have that the slope is m = 7/9 and the y-intercept is b = 12, we can write the equation of the line in slope-intercept form:
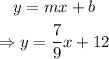
to find three coordinate points, we can use arbitrary values on x to get the y-coordinate. To make things easier, let's use x = 9, 18 and 27:
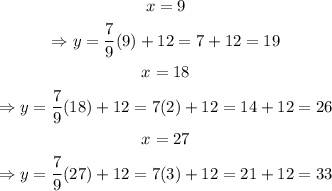
therefore, the line with slope m = 7/9 and y-intercept 12 passes through the three points (9,19), (18,26) and (27,33)