Question

Find the maximum or minimum value of f(x) = 2x^2 + 16x + 30.

Answer 1

The given function is

`f(x)=2x^2+16x+30`

To find the minimum of this function, we have to find the vertex of the parabola V(h,k). Where

`h=-(b)/(2a),k=f(h)`

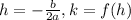
Where a = 2, and b = 16. Replacing these values, we have

`h=(-16)/(2(2))=-(16)/(4)=-4`

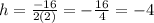
Then, we find k

`k=f(-4)=2(-4)^2+16(-4)+30=2(16)-64+30=-2`

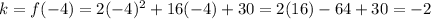
So, the vertex is at (-4, -2).

Therefore, the minimum of this function is at -2. Since the vertex is the lowest point of this parabola.