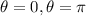Question

Can you please tell me a with this question I am reviewing for a final

Answer 1

Since the function of the difference between the length of spring and non-compressed length is

`f(\theta)=2cos\theta+√(3)`

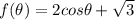
Part A:

If the two lengths are equal then the difference will be 0, then equate f(theta) by 0

`\theta\rightarrow theta`

`\begin{gathered} f(\theta)=0 \\ 2cos\theta+√(3)=0 \end{gathered}`

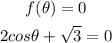
Subtract root 3 from both sides

`\begin{gathered} 2cos\theta+√(3)-√(3)=0-√(3) \\ 2cos\theta=-√(3) \end{gathered}`

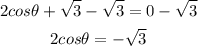
Divide both sides by 2

`\begin{gathered} (2cos\theta)/(2)=-(√(3))/(2) \\ cos\theta=-(√(3))/(2) \end{gathered}`

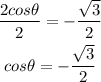
Since the values of cos are negative in the 2nd and 3rd quadrant, then we will find the value of theta on them

`\begin{gathered} \theta=\pi-cos^(-1)((√(3))/(2)) \\ \theta=\pi-(\pi)/(6)+2\pi n \\ \theta=(5\pi)/(6)+2\pi n \end{gathered}`
`\begin{gathered} \theta=\pi+(\pi)/(6)+2\pi n \\ \theta=(7\pi)/(6)+2\pi n \end{gathered}`

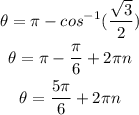
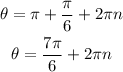
n is any integers

Part B:

We will replace theta with 2 theta

`\begin{gathered} 2\theta=\pi-(cos^(-1)(√(3))/(2)) \\ 2\theta=\pi-(\pi)/(6) \\ 2\theta=(5)/(6)\pi \\ (2\theta)/(2)=((5\pi)/(6))/(2) \\ \theta=(5\pi)/(12) \end{gathered}`
`\begin{gathered} 2\theta=\pi+cos^(-1)((√(3))/(2)) \\ 2\theta=\pi+(\pi)/(6) \\ 2\theta=(7\pi)/(6) \\ (2\theta)/(2)=((7\pi)/(6))/(2) \\ \theta=(7\pi)/(12) \end{gathered}`

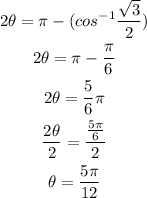
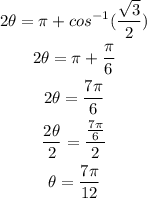
n = 1 because the interval from [0, 2pi]

Then the value of theta in part 2 is half the value of theta in part 1

The function with 2theta is

`f(2\theta)=2cos2\theta+√(3)`

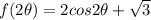
Part C:

The other given equation is

`g(x)=1-sin^2\theta+√(3)`

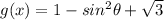
We will equate the two functions to find the time

`\begin{gathered} f(\theta)=g(\theta) \\ 2cos\theta+√(3)=1-sin^2\theta+√(3) \end{gathered}`

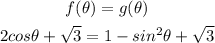
Subtract root 3 from both sides

`\begin{gathered} 2cos\theta+√(3)-√(3)=1-sin^2\theta+√(3)-√(3) \\ 2cos\theta=1-sin^2\theta \end{gathered}`

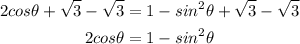
Since

`1-sin^2\theta=cos^2\theta`

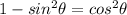
Then

`2cos\theta=cos^2\theta`

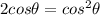
Subtract 2cos theta from both sides

`\begin{gathered} 2cos\theta-2cos\theta=cos^2\theta-2cos\theta \\ 0=cos^2\theta-2cos\theta \end{gathered}`

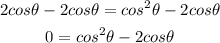
Take cos theta as a common factor

`\begin{gathered} cos\theta((cos^2\theta)/(cos\theta)-(2cos\theta)/(cos\theta))=0 \\ cos\theta(cos\theta-2)=0 \end{gathered}`

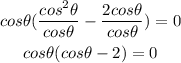
Equate each factor by 0 to find the value of theta

`\begin{gathered} cos\theta=0 \\ \theta=0,\theta=\pi \end{gathered}`
`\begin{gathered} cos\theta-2=0 \\ cos\theta-2+2=0+2 \\ cos\theta=2\rightarrow neglect\text{ it because 0}\leq cos\theta\leq1 \end{gathered}`

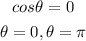
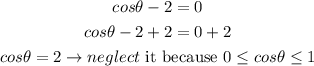
Then they have the same length at the time

`\theta=0,\theta=\pi`