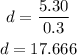Let n and d be the number of nickels and dimes, respectively. Since the total values is $5.40, we can write
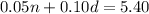
On the other hand, since the number of nickels is two less than four times the number of dimes, we have
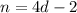
Then, we have the following system of equations:
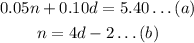
Solving by substitution method.
By substituting equation (b) into (a), we have
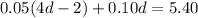
By distributing 0.05 into the parenthesis, we have
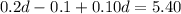
and by combining similar terms, we have
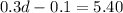
then, we have
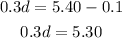
By dividing both sides by 0.3, we get