Question

Use the Factor Theorem to determine whether x-2 is a factor of P(x) = 2x³ - 4x²-x+7. Specifically, evaluate P at the proper value, and then determine whether x-2 is a factor.

Answer 1

Step 1:

In mathematics, factor theorem is used when factoring the polynomials completely. It is a theorem that links factors and zeros of the polynomial. According to factor theorem, if f(x) is a polynomial of degree n ≥ 1 and 'a' is any real number, then, (x-a) is a factor of f(x), if f(a)=0.

Step 2:

Write the polynomial function.

`p(x)\text{ = 2x}^3-4x^2-x+7`

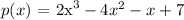
Step 3

x - 2 , substitute x = 2 into the polynomial.

`\begin{gathered} p(2)\text{ = 2}*2^3-4*2^2-2+7 \\ p(2)\text{ = 16 - 16 - 2 + 7} \\ p(2)\text{ = 5} \end{gathered}`

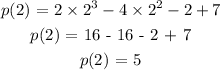
Final answer

x -2 is not a factor of p(x).