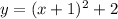Step 1. The first step is to find the vertex of the parabola, and another point (the y-intercept) located on the parabola.
Those points are:
Where the point is the y-intercept (0,3) and the vertex is at (-1,2)
Step 2. Label the vertex as (h,k)
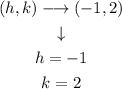
Step 3. Label the point as (x,y):
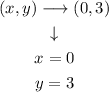
Step 4. Use the vertex form of the quadratic equation:
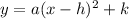
Where h and k are related to the vertex of the parabola.
From this equation, we need to find the value of a.
We find the value of a by substituting the values from step 3 and step 2:
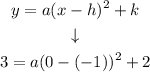
Solving for a:
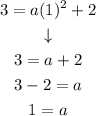
The value of a is 1.
Step 5. The final step is to go back to the vertex form of the quadratic equation:
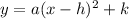
and substitute the known values for a, h and k:
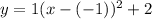
Simplifying:
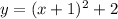
This is the equation of the graph.
Answer: