Question

Geometry parallel lines and transversal solve. Find the values of x and y.

Answer 1

1) The angles 3x - 5 and 4x - 29 are alternate interior angles, so they are congruent:

`\begin{gathered} 3x-5=4x-29 \\ 4x-3x=-5+29 \\ x=24 \end{gathered}`

2) The angles 10x and 5x are interior angles on the same side of the transversal (5x and 12y are as well), so they are supplementary angles:

`\begin{gathered} 10x+5x=180 \\ 15x=180 \\ x=(180)/(15)=12 \\ \\ 5x+12y=180 \\ 5\cdot12+12y=180 \\ 60+12y=180 \\ 12y=120 \\ y=(120)/(12)=10 \end{gathered}`

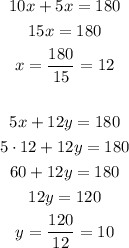
3) The angles 3x - 13 and 2x + 7 are alternate exterior angles, so they are congruent:

`\begin{gathered} 3x-13=2x+7 \\ 3x-2x=7+13 \\ x=20 \end{gathered}`

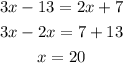
4) The angles 14x - 56 and 6x are corresponding angles, so they are congruent:

`\begin{gathered} 14x-56=6x \\ 14x-6x=56 \\ 8x=56 \\ x=(56)/(8)=7 \end{gathered}`

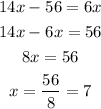
5) The angles 5x + 8 and 12x + 2 are exterior angles on the same side of the transversal, so they are supplementary:

`\begin{gathered} 5x+8+12x+2=180 \\ 17x=180-8-2 \\ 17x=170 \\ x=(170)/(17)=10 \end{gathered}`

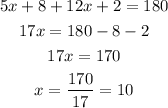
6) The angles 5x + 25 and 3x - 5 are interior angles on the same side of the transversal, so they are supplementary angles:

`\begin{gathered} 5x+25+3x-5=180 \\ 8x=180-25+5 \\ 8x=160 \\ x=(160)/(8)=20 \end{gathered}`

7) The angles 5x + 2 and 2x + 10 are interior angles on the same side of the transversal (2x + 10 and 4y + 8 are as well), so they are supplementary angles:

`\begin{gathered} 5x+2+2x+10=180_{} \\ 7x=180-12 \\ 7x=168 \\ x=(168)/(7)=24 \\ \\ 2x+10+4y+8=180 \\ 4y+2\cdot24+18=180 \\ 4y=180-48-18 \\ 4y=114 \\ y=(114)/(4)=28.5 \end{gathered}`

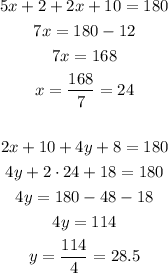
8) The angles 6x + 54 and 90 are alternate exterior angles, so they are congruent:

`\begin{gathered} 6x+54=90 \\ 6x=90-54 \\ 6x=36 \\ x=(36)/(6)=6 \end{gathered}`

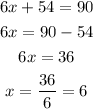
9) The angle 7x + 19 is corresponding to the angle supplementary to 4x - 15, so these angles are also supplementary:

`\begin{gathered} 7x+19+4x-15=180 \\ 11x=180-4 \\ 11x=176 \\ x=(176)/(11)=16 \end{gathered}`

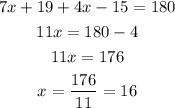
10) The angles 3x + 19 and 7x - 9 are vertically opposite angles, so they are congruent:

`\begin{gathered} 3x+19=7x-9 \\ 7x-3x=19+9 \\ 4x=28 \\ x=(28)/(4)=7 \end{gathered}`