Question

3^x-3^-x = 10help me solve this please

Answer 1

`3^x-3^(-x)\text{ = 10}`
`u=3^x`
`u-u^(-1)\text{ = 10 = u - }(1)/(u)=(u^2-1)/(u)=10`
`u^2-1\text{ = 10u}`
`u^2-10u\text{ - 1 = 0}`

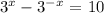
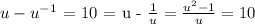
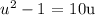
Using the quadratic formula, we found two solutions: u = 5 + sqrt(26) and u = 5 - sqrt(26)

u = 5 + sqrt(26) ==> 3^x = 5 + sqrt(26) ==> x = ln(5 + sqrt(26))/ln(3) = 2.104872087

u = 5 - sqrt(26) ==> 3^x = 5 - sqrt(26) has no solution because it ia a negative number and 3^x can not be a negative number

Answer:

x = 2.104872087