Question

two cards are selected from a standard deck of cards. The first card is not replacedbefore the secondcards is selected.Find the probability of selecting a 2 and then selectinga a king

Answer 1

A standard deck of cards has 52 total cards, 4 cards that are "2" and 4 card that are "king".

In the first selection, we have 4 "2" to pick from 52 prossibilities, so the probability of the first selection is:

`(4)/(52)=(1)/(13)`

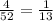
In the second pick, we have 4 "kings" to pick from 51 possibilities, since the first selection wasn't replaced. so, the probability of the second selection if:

`(4)/(51)`

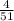
The probability of both happening in succession is the multiplication of the two probabilities:

`(1)/(13)\cdot(4)/(51)=(4)/(663)`

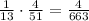
So, the probability of selection a "2" and then selection a "king" is 4/663, which is appproximately 0.00603 or 0.603%.