Question

I am needing help with problems 1 and 2. I’m definitely stuck and confused on where to start

Answer 1

1.

We need to write y = x^2 -2x - 5 in vertex so as to be able to determine the vertex and the axis of symmetry.

To do that, we need to write in the form y = a(x - h)^2 + k -----(1)

`\begin{gathered} y=x^2-2x-5=x^2-2x+(-(2)/(2))^2-(-(2)/(2))^2-5 \\ \\ \Rightarrow y=x^2-2x+1-1-5 \\ \\ \Rightarrow y=x^2-2x+1-6 \\ \\ \Rightarrow y=(x-1)^2-6\text{ -----\lparen2\rparen} \end{gathered}`

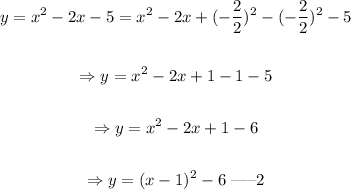
Comparing equation (2) with equation (1)

here a = 1, h = 1, k = -6.

Therefore, the vertex is: (1, -6)

The axis of symmetry is: x = h

Therefore, the axis of symmetry is x = 1.

Question 2)

The height function is given as;

`H(t)=-16t^2+16t+32`

To find out how long Jason will hit the water, we need to set H(t) = 0;

`\begin{gathered} \Rightarrow-16t^2+16t+32=0 \\ \\ \Rightarrow-16(t^2-t-2)=0 \\ \\ \Rightarrow t^2-t-2=0 \\ \\ \Rightarrow(t-2)(t+1)=0 \\ \\ \Rightarrow t=2,t=-1 \end{gathered}`

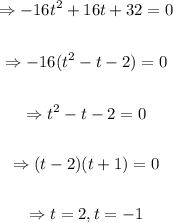
since negative time is not lucid, t = 2 is cogent.

Therefore, it will take 2 seconds for Jason to hit the water.