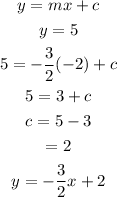Question

Select the correct answer from each drop down menu consider the given equation.3x+2y=8

Answer 1

Answer: the equation y= -3/2 x + 2 represents the line paralel to the given equation and passes through the point (-2,5)

Explanation:

Answer 2

`\begin{gathered} m=-(3)/(2) \\ c=2 \end{gathered}`

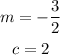
EXPLANATION

Given;

`3x+2y=8`

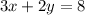
Re-write the equation in the standard form;

`\begin{gathered} y=mx+c \\ 3x+2y=8 \\ 2y=-3x+8 \end{gathered}`

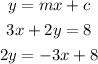
solve for y by dividing both sides by 2;

`\begin{gathered} 2y=-3x+8 \\ (2y)/(2)=-(3x)/(2)+(8)/(2) \\ y=-(3)/(2)x+4 \\ m=-(3)/(2) \end{gathered}`

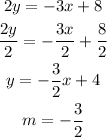
The line parallel to this line must have the same slope. Hence, the equation of the line that passes through points (-2,5) is;

`\begin{gathered} m=-(3)/(2) \\ y=5 \\ y=mx+c \end{gathered}`

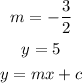
Substitute the value of point y and the slope;

`\begin{gathered} y=mx+c \\ y=5 \\ 5=-(3)/(2)(-2)+c \\ 5=3+c \\ c=5-3 \\ =2 \\ y=-(3)/(2)x+2 \end{gathered}`