Question

What are the domain and range of the real-valued function f(x) = -3 + √√4x - 12?The domain is x ≥ 3, and the range is f(x) ≤ - 3.The domain is x ≥ 3, and the range is f(x) > - 3.The domain is x ≤ 3, and the range is f(x) ≥ - 3.O The domain is x ≥ 3, and the range is all real numbers.

Answer 1

Given: A real-valued function

`f(x)=-3+√(4x-12)`

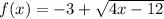
Required: Domain and Range of the function.

Explanation:

Domain of the function is all the values of x, for which the function is defined.

Here, root function is defined when 4x-12 is greater than equal to zero.

So domain is

`\begin{gathered} 4x-12\ge0 \\ 4x\ge12 \\ x\ge3 \end{gathered}`

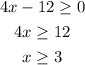
Thus, domain is

`x\ge3`

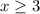
Now, for range

`\begin{gathered} 3\leq x<\infty \\ 12\leq4x<\infty \end{gathered}`

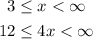
Further, subtracting 12

`\begin{gathered} 0\leq4x-12<\infty \\ 0\leq√(4x-12)<\infty \end{gathered}`

Adding -3

`\begin{gathered} -3\leq-3+√(4x-12)<\infty \\ -3\leq f(x)<\infty \end{gathered}`

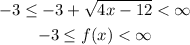
Thus range is

`f(x)\ge-3`

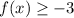
Final answer: Option 3 is correct answer.