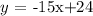Question

Hello, I need help with this problem.How do I write the slope-intercept form for the line that passes through the point (1,9) and has a slope of -15?

Answer 1

The slope-intercept form of a line with slope m and y-intercept b is given by the following equation:

`y\text{ = mx+b}`

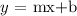
According to this, the provisional equation of the line would be:

`y\text{ = -15x+b}`

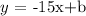
Now, to find b, we can take any point (x,y) on the line and replace its coordinates into the above equation, and then we can solve for b. For example, we can take the given point (x,y) = (1,9) and obtain:

`9\text{ = -15(1)+b}`

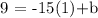
this is equivalent to:

`9\text{ = -15+b}`

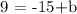
solving for b, we obtain:

`b\text{ = 9+15= 24}`

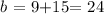
then, we get that:

`b\text{ = 24}`

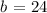
So that, we can conclude that the slope-intercept form for the line that passes through the point (1,9) and has a slope of -15 is:

`y\text{ = -15x+}24`

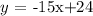
Then, the correct answer is:

`y\text{ = -15x+}24`