Given the following equation of the hyperbola:
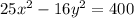
The standard form of the hyperbola will be as follows:
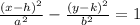
We will rewrite the given equation to be like the standard form:
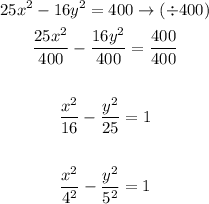
Compare the last equation with the standard form:
So, the answer will be as follows:
The value of h = 0
The value of k = 0
The value of a = 4
The value of b = 5