Question

EspanolA flower garden is shaped like a circle. Its radius is 15 yd. A ring-shaped path goes around the garden. Its outer edge is a circle with radius 18 yd.15 yd18 ydG 回回國The gardener is going to cover the path with sand. If one bag of sand can cover 8 yd?, how many bags of sand does the gardener need? Note that sand comesonly by the bag, so the number of bags must be a whole number. (Use the value 3.14 for 1.)

Answer 1

We have a path which has an area that is the difference between the outer circle (r = 18 ft) and the inner circle (r = 15 ft), showed as the shaded area.

Then, we can express the area of the path (A) as:

`\begin{gathered} A=A_o-A_i \\ A=\pi r^2_o-\pi r^2_i \\ A=\pi(r^2_o-r^2_i) \\ A\approx3.14(18^2-15^2) \\ A\approx3.14(324-225) \\ A\approx3.14\cdot99 \\ A\approx310.86\text{ yd}^(2) \end{gathered}`

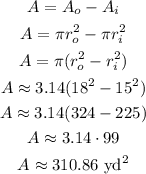
Ao: area of the outer circle

Ai: area of the inner circle

ro: radius of the outer circle

ri: radius of the inner circle

As the path has an area of 310.86 square yard and a bag of sand covers 8 square yard per bag, we can calculate the number of bags (n) dividing the path area by the area covered by one bag:

`n=(A)/(b)=\frac{310.86yd^2}{\frac{9yd^2}{\text{bag}}}=34.54\text{ bags}\approx35\text{ bags}`

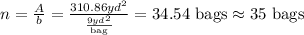
Answer: 35 bags of sand are needed.