In order to calculate how many students played one or more of the three sports, we can use the formula below:
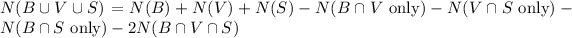
From the given information, we have:
N(B) = 25
N(V) = 22
N(S) = 23
N(B and V only) = 2
N(V and S only) = 3
N(B ans S only) = 1
N(B and V and S) = 6.
So we have:
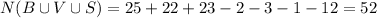
Therefore the number of students that play at least one sport is 52.