Question

Identify the vertex, the axis of symmetry and all intercepts.g(x)=x^2-6x-1

Answer 1

the vertex (h, k) = (3, -10)

The axis of symmetry is 3

y-intercept is (0, -1)

x intercepts are x = 6.1623, x = -0.1623

Step-by-step explanation:
`\begin{gathered} \text{The given function:} \\ g\mleft(x\mright)=x^2-6x-1 \end{gathered}`

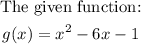
To answer the question, let's plot the graph of the function:

The tip of the parabola is the vertex. From the graph, the tip is at x = 3, y = -10

Hence, the vertex (h, k) = (3, -10)

The axis of symmetry is the value of x at the vertex. This divides the parabola into equal halves.

x coordinate at the vertex is 3

The axis of symmetry is 3

y-intercept is the value of y when x = 0

`\begin{gathered} g(x)\text{ = }x^2-6x-1 \\ at\text{ x = 0} \\ g(0)=0^2\text{ - 6(0) - 1} \\ g(0)\text{ = -1} \\ y-\text{intercept is -1} \end{gathered}`

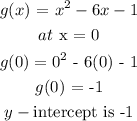
In interval notation, y-intercept is (0, -1)

x intercept is the value x when y = 0

`\begin{gathered} g\mleft(x\mright)=x^2-6x-1 \\ 0\text{ }=x^2-6x-1 \\ a\text{ = 1, b = -6, c = -1} \\ x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x\text{ = }\frac{-(-6)\pm\sqrt[]{(-6)^2-4(1)(-1)}}{2(1)} \\ x\text{ = }\frac{6\pm\sqrt[]{36+4}}{2}\text{ = }\frac{6\pm\sqrt[]{40}}{2} \\ x\text{ = }\frac{6\pm2\sqrt[]{10}}{2}\text{ = }\frac{2(3\pm\sqrt[]{10}\text{ )}}{2}\text{ } \\ x\text{ = }3\pm\sqrt[]{10} \\ x\text{ = }3+\sqrt[]{10}\text{ or }3-\sqrt[]{10} \\ x\text{ = 6.1623 or x = -0.1623} \end{gathered}`

If we check, the graph, that is the value of x when the line crosses the x axis. This is how it is gotten

Hence, x intercepts are x = 6.1623, x = -0.1623