Question

Given the function h(x) below, select the answer choice which correctly decomposes h(x) into component functions f(x) and g(x) so that h(x)=f(g(x)).h(x)=(3x−5)2 Question 9 options:h(x)=f(g(x)), where f(x)=x2 and g(x)=3x−5h(x)=f(g(x)), where f(x)=3x and g(x)=(x−5)2h(x)=f(g(x)), where f(x)=3x2 and g(x)=x−5h(x)=f(g(x)), where f(x)=x−5 and g(x)=3x2h(x)=f(g(x)), where f(x)=3x−5 and g(x)=x2

Answer 1

The correct option is:

h(x)=f(g(x)), where f(x)=x2 and g(x)=3x−5

Step-by-step explanation:

We have the function

`h(x)=(3x-5)^2`

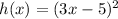
And we want to find the functions f and g such that:

`h(x)=f(g(x))`

We can see that in h(x) we have a parenthesis squared. If we define f as:

`f(x)=x^2`

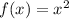
Then, the function f will square whatever we put in the function.

Now if we define:

`g(x)=3x-5`

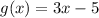
Now, if we evaluate f(x) on g(x):

`f(g(x))=(g(x))^2=(3x-5)^2=h(x)`

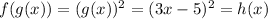
Thus, the correct answer is the first option