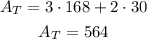Calculating the lateral area of a triangular prism is equivalent to calculating the area of a rectangle.
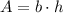
For this case the sides of the lateral area would be 14 and 12.

The lateral area of a prism triangle is repeated three times because we have three faces of the same proportions.
To calculate the total area the formula would be as follows
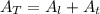
Where
AT = Total area
Al = Lateral area
At = Area of the front triangle
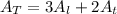
The area of the triangle can be calculated as follows
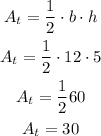
The total area would be