Question

A modified roulette wheel has 40 slots. One slot is 0, another is 00, and the others are numbered 1 through 38, respectively. You are placing a bet that the outcome is an odd number, (inroulette, 0 and 00 are neither odd nor even)a. What is your probability of winning?B. What are the actual odds against winning? C. How much profit should you make on the 15 dollar bet if you could somehow convince the casino to change its payoff odds so that they are the same as the actual odds against winning?

Answer 1

a) We win if the result is an odd number. There are 38/2 = 19 odd numbers and 40 total possible outcomes.

The probability of getting an odd number is given by:

`P(winning)=P\mleft(odd\mright)=\frac{\text{\# of odd outcomes}}{\text{\# total possible outcomes}}=(19)/(40)\text{.}`

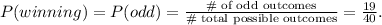
b) The odds against an event is equal to the ratio of the number of ways that cannot occur compared to in how many ways it can occur. So we have that:

Odds against winning = # of not winning outcomes/ # of winning outcomes = 21/19.

c) Now the payoff odds are the same as the actual odds against winning, 21/19. So a payoff odds of 21:19 mean a profit of $21 for every $19 bet. A winning bet of $15 means a profit of 21/19 * $15 ≅ $16.58.

Answers

a) The probability of winning is 19/40.

b) The actual odds against winning are 21:19.

c) The winning bet of $15 means a profit of approximately $16.59 if the payoff odds are the same as the actual odds against winning.