Question

A bathroom has a temperature of -.5 degrees F and heats up 15 degrees F. each hour. A closet has a temperature of -.25 degrees F. and it heats up 10 degrees F. each hour. For what number of hours will the bathroom be warmer than the closet?

Answer 1

after 0.05 hours the bathroom will be warmer than the closet

Step-by-step explanation

Step 1

Set the equations.

let x represents the number of hours, so

a)A bathroom has a temperature of -.5 degrees F and heats up 15 degrees F. each hour,so

`\begin{gathered} \text{temperature}=-0.5+(15\text{ degr}ees\text{ per hour)} \\ T_(bathroom)=-0.5+15x\Rightarrow equation\text{ (1)} \end{gathered}`

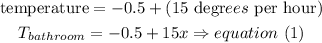
b)A closet has a temperature of -.25 degrees F. and it heats up 10 degrees F. each hour, so

`\begin{gathered} \text{Temperature}_(closet)=-0.25+(10\text{ degr}ees\text{ per hour)} \\ T_(closet)=-0.25+10x\Rightarrow equation(2) \end{gathered}`

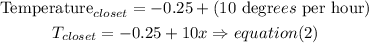
Step 2

For what number of hours will the bathroom be warmer than the closet?

to solve this we need to formule an inequality

`\begin{gathered} T_(bathroom)>T_(closet) \\ hence \\ -0.5+15x>-0.25+10x \end{gathered}`

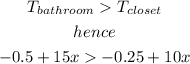
now, we need to solve the inequality

`\begin{gathered} -0.5+15x>-0.25+10x \\ \text{subtract x in both sides} \\ -0.5+15x-10x>-0.25+10x-10x \\ 5x-.5>-0.25 \\ \text{add 0.5 in both sides} \\ 5x-.5+0.5>-0.25+0.5 \\ 5x>0.25 \\ \text{divide both sides by 5} \\ (5x)/(5)>(0.25)/(5) \\ x>0.05\text{ hours} \end{gathered}`

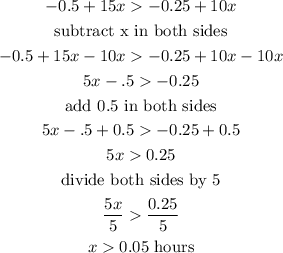
therefore, after 0.05 hours the bathroom will be warmer than the closet

I hope this helps you