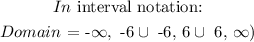Question

KIdentify any vertical, horizontal, or oblique asymptotes inthe graph of y=f(x). State the domain of f (interval notation).42-+12QQIdentify any vertical asymptotes. Select the correchoice below and, if necessary, fill in the answerboxes to complete your choice.OA. There is only one vertical asymptote. Itsequation is(Type an equation.)B. There are two vertical asymptotes. Theequation of the leftmost one is x=-6and the equation of the rightmost one isx=6(Type an equation.)OC. There are no vertical asymptotes.Identify any horizontal or oblique asymptotesSelect the correct choice below and, if necessary.fill in the answer box to complete your choice.OA. The function has a horizontal asymptotewhose equation is(Type an equation.)OB. The function has an oblique asymptotewhose equation is,(Type an equation.)C. The function has neither a horizontal noran oblique asymptote

Answer 1

Answer:

the function has a horizontal asymptote whose equation is y = -3 (option A)

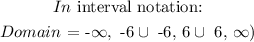
`\begin{gathered} In\text{ interval notation:} \\ Domain\text{ = \lparen-}\infty,\text{ -6\rparen }\cup\text{ \lparen-6, 6\rparen }\cup\text{ \lparen6, }\infty) \end{gathered}`Step-by-step explanation:

Given:

A graph of a rational function

To find:

a) if the graph has a horizontal or oblique asymptote

b) domain of f

A horizontal asymptote is a line that is not part of the function of the graph.

From the graph, there is a horizontal dashed line between y = -2 and y = -4.

None of the graphs touches this line. This is the horizontal asymptote. The equation at the asymptote is y = -3 (midpoint between -2 and -4)

Hence, the function has a horizontal asymptote whose equation is y = -3

The domain is the input of the function (x values). Since the function is not given, we will use the vertical asymptote to determine the domain.

The vertical asymptotes are x = -6 and x = 6

The domain of the function is all real numbers except x = -6 and x = 6

`\begin{gathered} In\text{ interval notation:} \\ Domain\text{ = \lparen-}\infty,\text{ -6\rparen }\cup\text{ \lparen-6, 6\rparen }\cup\text{ \lparen6, }\infty) \end{gathered}`