Question

Where to find descartes rule of signs and asymptote of a rational function outside of the classroom

Answer 1

To find a situation where we can apply the rule of signs we need a situation where there are polynomials in real life.

1. The first example is of an object thrown directly upwards. The height of an object in these instances can be found by:

`h(t)=h_0+v_0t-(g)/(2)t^2`

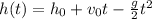
If the object is thrown from 1 m from the ground, with a 5 m/s speed. The height of the object can be found as:

`h(t)=-4.91t^2+5t+1`

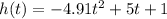
We can apply the Descartes rule to know how many positive real solutions the equation has. In this case a solution for the equation means that the object has reached the ground, because on those situations the height will be 0. The positive solution means the time it took for the object to reach the ground. These are the only solutions we can use, because there is no negative time. By the Descartes rule there is only one positive real solution, because there is one change in sign.

2. When a bucket of water containing 20 lb of water at 77° F is mixed with "x" lb of water at 190° F. The temperature of the water is given by:

`\begin{gathered} T=(M_a\cdot C_a\cdot T_a+M_b\cdot C_b\cdot T_b)/(M_aC_a+M_bC_b) \\ T=(20\cdot816.466141\cdot77+x\cdot816.466141\cdot190)/(20\cdot816.466141+x\cdot816.466141) \\ T=(1540+190x)/(20+x) \end{gathered}`

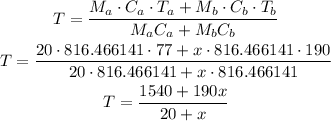
The temperature of the water on the bucket will rise approaching a thermal equilibrium approaching it asymptotically as shown below: