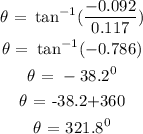Question

AcellusVector E is 0.111 m long in a90.0.º direction. Vector Fis0.234 m long in a300° direction.Find the magnitude of theirvector sum.magnitude (m)

Answer 1

Answer:

The magnitude of the vector sum = 0.149 m

The direction = 321.8 degrees

Step-by-step explanation:

Find the x and y components of vector E

`\begin{gathered} E_x=\text{ 0.111}\cos 90 \\ E_x=\text{ }0 \\ E_y=\text{ 0.111sin90} \\ E_y=\text{ }0.111 \\ E=E_xi+E_yj \\ E\text{ = 0.111j} \end{gathered}`

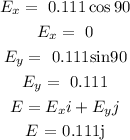
Find the x and y components of vector F

`\begin{gathered} F_x=\text{ 0.234}\cos 300 \\ F_x=\text{ }0.117 \\ F_y=\text{ 0.234}\sin 300 \\ F_y=\text{ }-0.203 \\ F=F_xi+F_yj \\ F\text{ = 0.117i-0.203j} \end{gathered}`

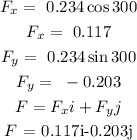
The vector sum of E and F is:

`\begin{gathered} E+F\text{ = 0.111j+(0.117i-0.203j)} \\ E+F=0.117i-0.092j \end{gathered}`

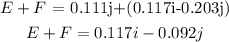
The magnitude of the vector sum is given as:

`\begin{gathered} |E+F|=\sqrt[]{0.117^2+(-0.092)^2} \\ |E+F|\text{ = }\sqrt[]{0.022153} \\ |E+F|=\text{ }0.149 \end{gathered}`

The magnitude of the vector sum = 0.149 m

The direction is given as:

`\begin{gathered} \theta\text{ = }\tan ^(-1)((-0.092)/(0.117)) \\ \theta\text{ = }\tan ^(-1)(-0.786) \\ \theta\text{ = }-38.2^0 \\ \theta\text{ = -38.2+360} \\ \theta\text{ = }321.8^0 \end{gathered}`