A line with slope m and that passes through the point (x₁, y₁) have the following point-slope form equation:

Furthermore, if this line passes through a second point (x₂, y₂), its slope is given by:

In this problem, the given line passes through points (6, 2) and (10, -1). So, we have:
x₁ = 6
y₁ = 2
x₂ = 10
y₂ = -1
Then, using those values to find m, we obtain:
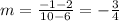
And the equation of the line, in point-slope form, is:

Therefore, option A is correct.