Question

You play a game that requires rolling a six-sided die then randomly choosing a colored card from a deck containing 5 red cards, 7 blue cards and 8 yellow cards. Find the probability that you will roll a 6 on the die and then choose a blue card.answers: 7/1201/61/207/20

Answer 1

The question tells us there is a rolling die with 6 faces.

This means that the probability of getting any number after rolling the die is equal for all values of die.

i.e.

`\begin{gathered} P(\text{any value on die)=}(1)/(6) \\ \\ i\mathrm{}e\text{.} \\ P(1)=(1)/(6) \\ P(2)=(1)/(6) \\ P(3)=(1)/(6) \\ \\ \ldots\text{and so on} \end{gathered}`

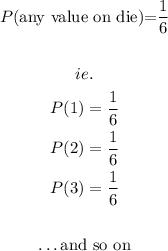
The number of cards in the deck is: 5 red + 7 blue + 8 yellow = 20 cards altogether.

Thus, if we pick a blue card from this deck of 20 cards, the probability is:

`\begin{gathered} P(\text{blue)}=\frac{n\text{umber of blue cards}}{\text{total number of cards}} \\ \\ P(\text{blue)}=(7)/(20) \end{gathered}`

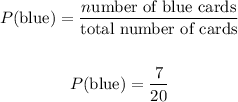
Therefore, if these two events - rolling a die and picking a blue card - occur at the same time, then we use the AND probability to solve.

This is done below: